////////////////////////////////////////////////////////////////////////////////////////////////
TRANSFORM and Conquer ?
Transform's basic concept is that it modifies the problem to make it more amenable to solution.
Example
{ 1 }
Balanced Search Tree
AVL tree is for every node,
the difference between the heights of its left and right subtrees (called the balance factor) is 0 or 1.
AVL tree maintain their balance using rotations.
So, extra memory is needed to maintain node's balance.
ROTATION
-
Single R-rotation
rotate tree to clockwise. -
Single L-rotation
rotate tree to counter-clockwise. -
Double LR-rotation
rotate tree to clockwise and change parent node with left-child node. -
Double RL-rotation
rotate tree to counter-clockwise and change parent node with right-child node.
Heap Sort
{ 2 }
heap sort is essentially complete.
The root is the largest number.
-
Build Heap
-
Remove key : heap delete root, and insert the last key(right-most) at place of root.
-
Then fix correctly : Root must be largest key
{ 0 }
Other algorithms
-
Presorting
-
Gaussian Elimination
-
Linear programing(Wyndor Glass)
-
Spacing problem
-
Knapsack problem
-
Input : external file 'input.txt'
So, write code for reading the external file. -
Problem reduction.
We do not need another people except our friend.
So, except the another people. -
Then, find the friend and fix the phone number into new number.
-
Output : save the output as external file.
GROUP PROJECT
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
My friend's Phone number is changed
What kind of Transform and Conquer?
-
Instance simplification (simpler instance)
The same problem make more easily or transform for easy use.
ex)Presorting, Gaussian Elimination
-
Representation change (another representation)
Changing the same problem in other representations
ex) Balanced Tree( AVL tree, 2-3 tree), heap
-
Problem reduction (another problems's instance)
To apply the already available algorithms, transform original problem as other problems.
ex) reductions to graph problems, linear programming
binary search tree is marred by the bad (linear) worst-case efficiency.
Two ideas to overcome it are

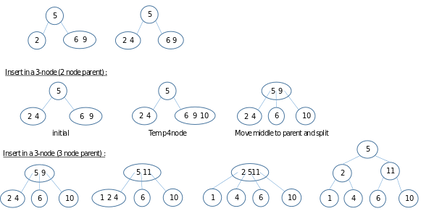
Multiway Search Tree is that allows more than one key in the one node.
2-3 tree is that has 2 nodes or 3 nodes
-
Insert the key into node
-
If there are 3 keys in one node, middle key become the parent node.
-
Then, insert again, but now there is 3 division (smaller, larger, between)